[CMU 15-445]HyperLogLog原理

HyperLogLog in Presto

情景

想要确定一个有重复元素的很大集合的cardinality。常规方法的时间开销或者内存开销过大，无法接受。

A simple estimator

首先，生成一个理论数据集：

• 生成n个均匀分布在[0,1]之间的数。
• 随机挑选一些数，随机复制几次。
• 打乱顺序

因为所有数是均匀分布的，可以找出最小的数$x_{min}$，然后估计集合的$cardinality = 1/x_{min}$.

为了确保数是均匀分布的，可以对每个数进行哈希，然后根据哈希值来估计。

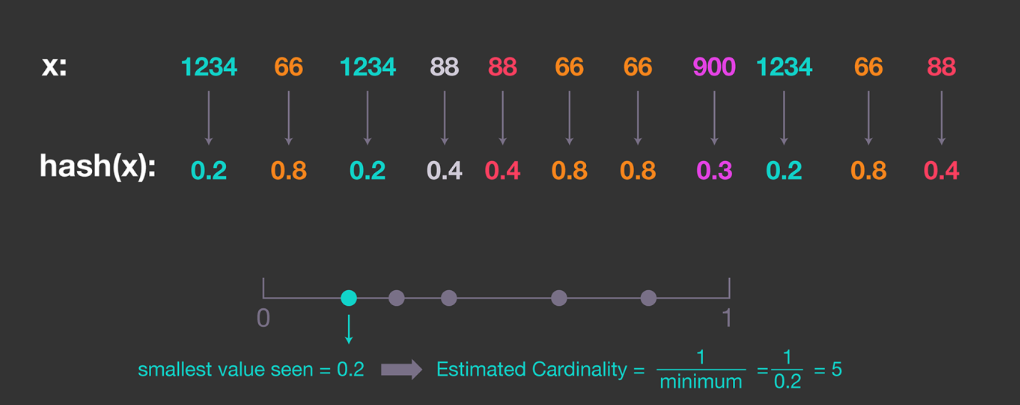
这种简单的估计有较高的偏差，因为如果最小值太小，会导致估计的值过大。

Probabilistic counting

为了改善上述问题，我们可以通过统计哈希值二进制开头连续的0的个数。因为某个给定哈希值开头连续出现$i$个0的概率是$1/2^i$。也就是说，平均来说，每$2^i$个哈希值才会出现一个连续$i$个0的哈希值。

因此，我们可以统计所有哈希值中出现的最大的连续的0的个数$k$，然后集合的$cardinality=2^k$。

这种方法有两个缺点：

• 最好情况下，该方法估计的值只能是2的幂
• 因为该方法仍然只依赖于某个有最长连续0的哈希值，因此也有较大的偏差。

这种方法的优点是需要的内存空间很小，只需要记录最大连续的0的个数即可。

Improving accuracy：LogLog

我们可以设计很多哈希函数，然后将最大连续0的个数取平均。但是这种方法的计算开销过大。

另一种方法是，用哈希值的最高几位作为索引，索引到一个bucket，每个bucket记录其见过的最长连续0的个数。然后用公式$cardinality = constant · m · 2^{1/m \Sigma^N_{j=1}R_j}$来进行估计。

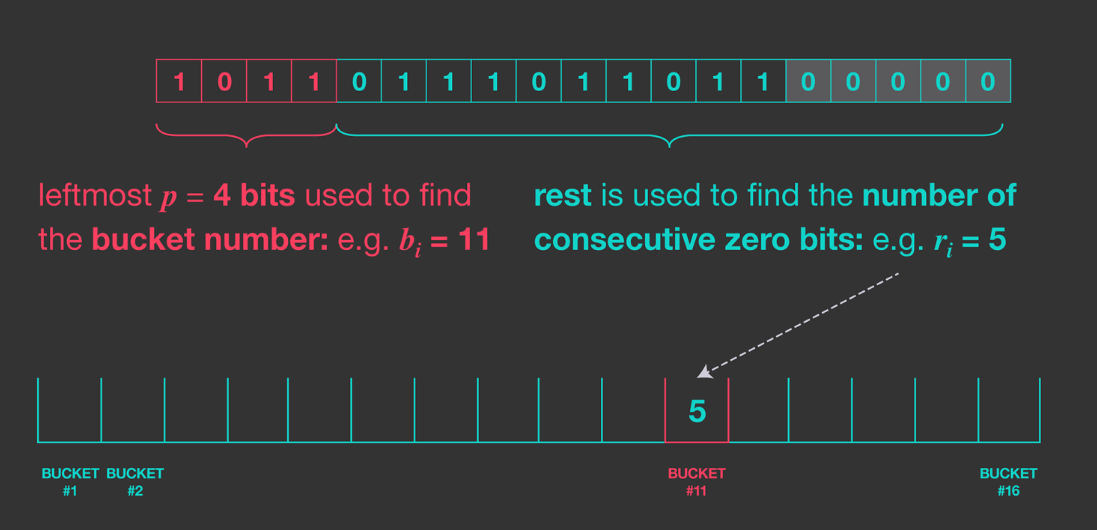
统计分析指出上述方法的估计有一个偏差，因此令$constant = 0.79402$来修正这个偏差。

对于$m$个bucket，该方法的误差大概在$1.3/\sqrt{m}$左右。

HLL：Improving accuracy further

• 异常值会降低准确度。因此，可以在收集每个bucket的值的时候，只考虑较小的70%的bucket，扔掉其余30%。这种算法（SuperLogLog），可以将误差降低到$1.05/\sqrt{m}$.
• HLL使用调和平均，可以将误差降低到$1.04/\sqrt{m}$左右。

最终，得到的公式为
$$
CARDINALITY_{HLL} = constant · m · \frac{m}{\Sigma_{j=1}^N 2^{-R_j}}
$$
集合并运算

对于两个HLL数据结构，我们可以对其进行并操作（对每个对应位置的bucket取二者的较大者）。该操作很简单并且是无损的。对于并行运算友好。

Presto‘s HLL implementation

该实现方法有两种布局：sparse和dense。

sparse布局的结果几乎是准确的，但是对于cardinality较大的情况，算法会自动采用dense布局，该布局的结果是上述HLL算法的预估值。

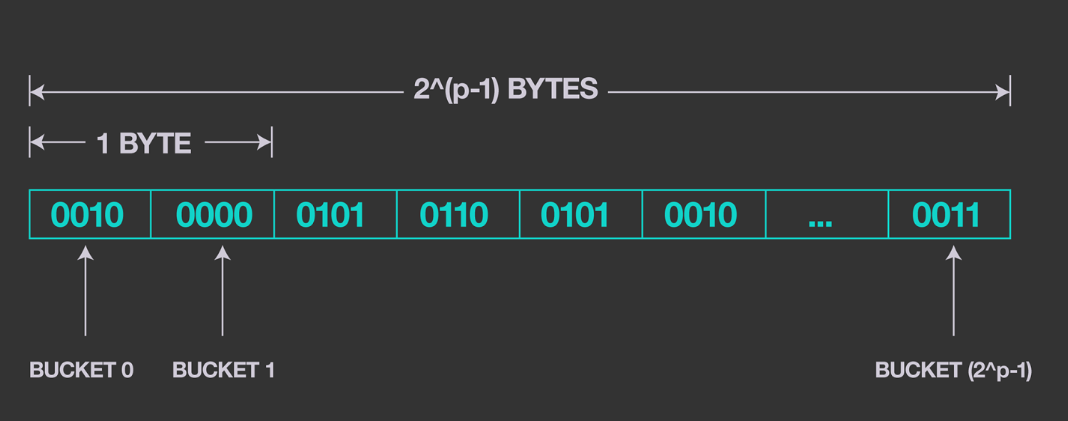
稀疏布局存储一组相邻的 32 位的bucket，按桶索引升序排序。当有新数据输入时，Presto 会检查数据桶编号是否已经存在。如果存在，则更新其值。如果数据桶是新的，Presto 会分配一个新的 32 位内存地址来保存该值。随着数据量的增加，存储桶的数量可能会超过预先设定的内存限制。这时，Presto 会切换到密集布局表示法。

密集布局 有固定数量的存储桶，相关内存从一开始就被分配。桶值以 4 位值序列的形式编码，如下图所示。根据 HLL 算法的统计特性，4 位足以编码给定 HLL 结构中的大部分值。对于大于4位的值，余数存储在溢出项列表中。