[算法]快速幂算法

快速幂算法

1 题目

设$a$是一个给定实数，计算$a^n$，其中$n$是自然数。

2 解法

2.1 暴力解

暴力解比较直观，直接对$a$进行$n-1$次相乘即可。

时间复杂度为$O(n)$.

2.2 快速幂-递归

考虑分治的方法，首先将问题规约为一个更小的子问题，计算$a^{n/2}$，计算出的结果只需要在相乘一次即可得到原问题的解。这里需要对$n$的奇偶性进行分情况讨论，如下所示：
$$
\begin{align}
& a^n = a^{n / 2} \times a^{n / 2} \qquad n为偶数 \\
& a^n = a^{(n - 1) / 2} \times a^{(n - 1) / 2} \times a \qquad n为奇数
\end{align}
$$
时间复杂度

该递归算法的递推方程为
$$
W(n) =
\begin{cases}
& W(n/2) + O(1) \\
& W(1) = 0
\end{cases}
$$
该递推方程符合主定理的第二种情况，由此可得该算法在最坏情况下的时间复杂度$W(n) = O(logn)$.

代码

double fastExponentiation(double a, unsigned n)
{
    if (n == 0) return 1;
    auto result = fastExponentiation(a, n / 2);
    if (n % 2 == 0) return result * result;
    else return result * result * a;
}

2.3 快速幂-迭代

观察递归版本，对于$a^{10}$，我们发现，快速幂计算$a^{10}$的过程如下：
$$
a^{10} = (a^5)^2 = (a^2 * a^3)^2 = ((a * a)^2 * a)^2
$$
因为两个同底的幂相乘可以转换为指数相加，因此为了计算$a^n$，我们只需要求出一个序列$d_n = [d1, d2, …, d_k]$，使得${\Sigma_{i=1}^{k}d_i} = n$，如此，我们可以通过求解$a^{d_i}$，并将所有结果累乘获得原问题的解。

那么，如何求得这个序列$d_n$呢？最简单的方法是将$n$表示成二进制形式，所有二进制位为1的权组成的集合即我们要求的$d_n$.

时间复杂度

我们将求解过程融入到求一个数的二进制表示的过程中，因此最坏时间复杂度为$W(n) = O(logn)$，

代码

double fastExponentiation(double a, unsigned n)
{
    unsigned bit = 0;  
    double res = 1;    
    while (n > 0)
    {
        bit = n % 2;
        n >>= 1;
        if (bit) res *= a;
        a *= a;
    }
    return res;
}

3 扩展

该思想可以用于求解Fibonacci数列。

定理

设$Fn$为第$n$个Fibonacci数，那么有

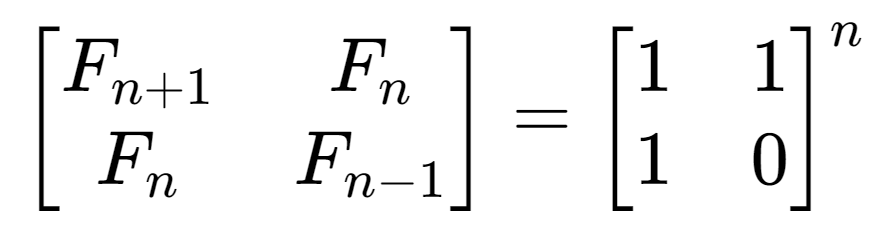
通过数学归纳法可以证明上述定理。

由定理，我们可以将计算Fibonacci数转换为矩阵的$n$次幂，因为计算二阶矩阵相乘只需要8次乘法，即常数时间，因此我们可以优化求Fibonacci数的算法时间复杂度到$O(logn)$.